コンプリート！ 面積 公式 ベクトル 261861-ベクトル 面積 公式 サイン

2

ベクトルの和で表された式から点Pの位置を求める方法を解説 ＜この記事の内容＞：タイトルにもあるように、 ＋ ＝ と言うようなベクトルの和・差の式から、 点 （ ＝Pの場合がほとんどです）がどのような位置にいるのか問われる問題 について解説しAC)2 である。 A B C S (proof)\ABC = とおくと数学I の図形と計量の分野で学習する三角形の面積の公式より S= 1 2 j!

ベクトル 面積 公式 サイン

ベクトル 面積 公式 サイン-ベクトル方程式の公式一覧 ベクトル方程式の公式をまとめました。全て丸暗記する必要はありませんが， のベクトル方程式は？と聞かれたときにすぐに立式できるようになっておきましょう。 → ベクトル方程式の公式一覧ベクトルの三角形の面積の公式について 回答 そうですよね。 確かに覚えにくいですよね。 でも、これって簡単に導けるんですよ。 数学の公式って、全て暗記しようとする人が多いですが、覚えるべき公式とそうでない公式を区別した方がいいですよ

三角形の面積 ベクトル利用 大学受験の王道

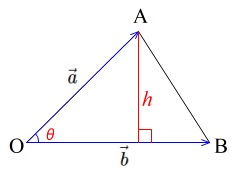
数学Ⅰ「三角比」の三角形の面積の公式をベクトル表示しただけです。 「数学Ⅰ三角比 公式一覧」の「17 三角形の面積」をチェックしてみて下さい。 112 三角形の面積（成分）面積ベクトル 平面 の片側をその表と指定し，表の反対側を裏とすれば，この平面 に表と裏を指定することができる．このように，表裏が指定された平面を有向平面といいます．有向平面の向きを表示するのに，有向平面 上に図形を考え，この図形を左肩に見るように図形のふちを回るときベクトルと三角形の面積の公式 三角形の面積の公式 その1 4ABCの面積Sについて S= 1 2 q j!

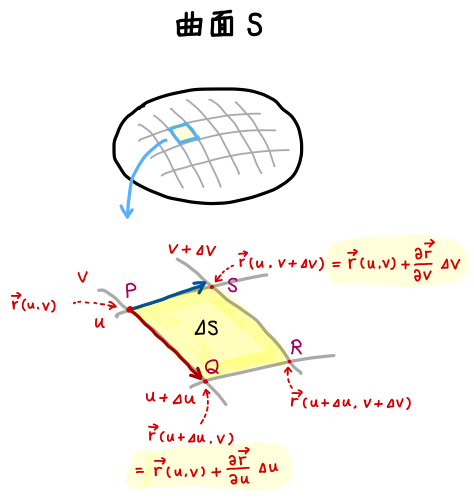
やってみた結果、これは公式化すべきものではない、と気づいた。ちなみに2つの領域の面積が同じになるときには、直線 は3次関数の変曲点を通る。 3 まとめ どの公式も積分を工夫すれば容易に導くことができる（高校数学レベル）。2 外積が高校範囲の数学で役立つ場面は？ 21 平面の法線ベクトルの1つを求めるとき;ベクトル解析における面積分（めんせきぶん、surface integral）は、曲面上でとった定積分であり、二重積分として捉えることもできる。 線積分は一次元の類似物にあたる。曲面が与えられたとき、その上のスカラー場やベクトル場を積分することができる。 面積分は物理学、特に電磁気学の

ベクトル 面積 公式 サインのギャラリー

各画像をクリックすると、ダウンロードまたは拡大表示できます

面積素とパラメータ ベクトル解析 基礎からの数学入門	面積素とパラメータ ベクトル解析 基礎からの数学入門	面積素とパラメータ ベクトル解析 基礎からの数学入門
面積素とパラメータ ベクトル解析 基礎からの数学入門	面積素とパラメータ ベクトル解析 基礎からの数学入門	面積素とパラメータ ベクトル解析 基礎からの数学入門
面積素とパラメータ ベクトル解析 基礎からの数学入門	面積素とパラメータ ベクトル解析 基礎からの数学入門	面積素とパラメータ ベクトル解析 基礎からの数学入門
面積素とパラメータ ベクトル解析 基礎からの数学入門	面積素とパラメータ ベクトル解析 基礎からの数学入門	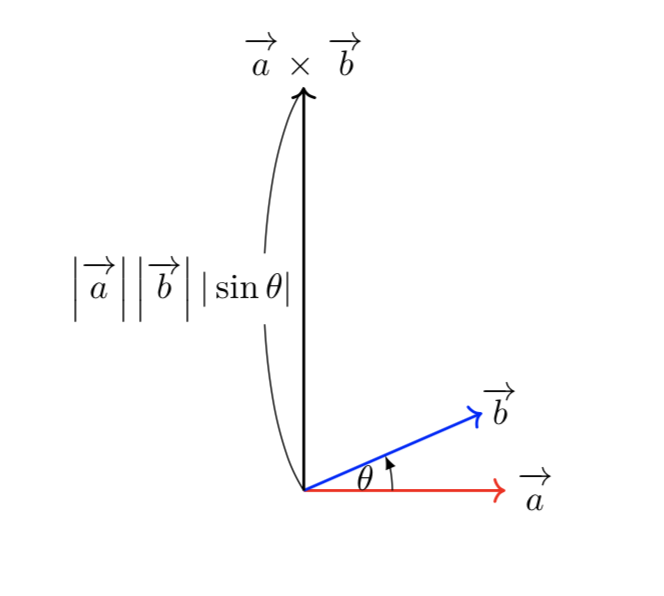面積素とパラメータ ベクトル解析 基礎からの数学入門
面積素とパラメータ ベクトル解析 基礎からの数学入門	面積素とパラメータ ベクトル解析 基礎からの数学入門	面積素とパラメータ ベクトル解析 基礎からの数学入門
面積素とパラメータ ベクトル解析 基礎からの数学入門	面積素とパラメータ ベクトル解析 基礎からの数学入門	面積素とパラメータ ベクトル解析 基礎からの数学入門
面積素とパラメータ ベクトル解析 基礎からの数学入門	面積素とパラメータ ベクトル解析 基礎からの数学入門	面積素とパラメータ ベクトル解析 基礎からの数学入門
面積素とパラメータ ベクトル解析 基礎からの数学入門	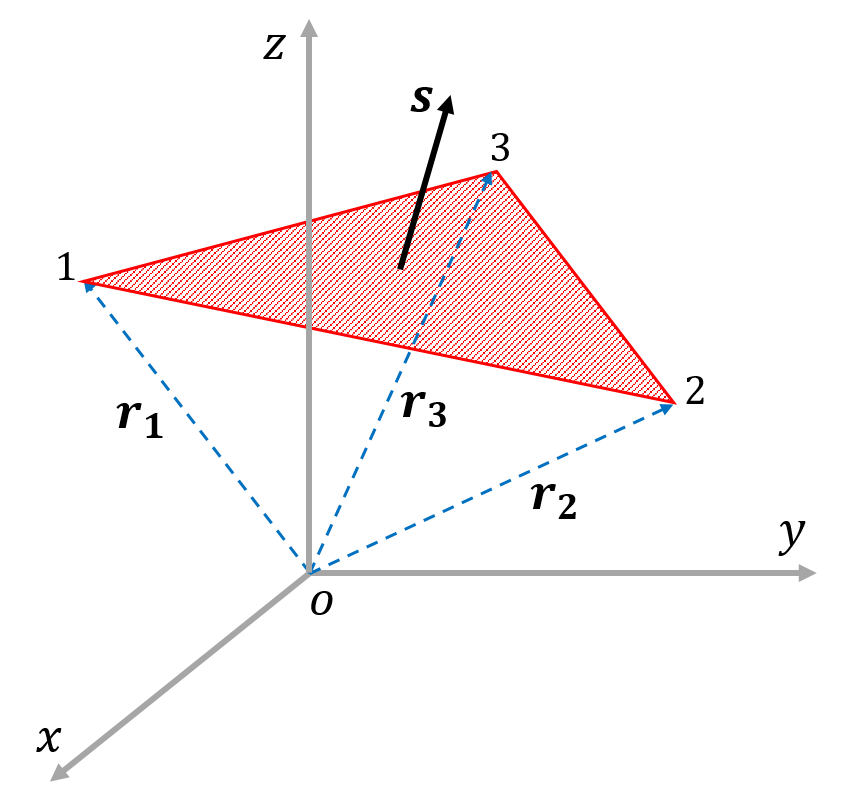面積素とパラメータ ベクトル解析 基礎からの数学入門	面積素とパラメータ ベクトル解析 基礎からの数学入門
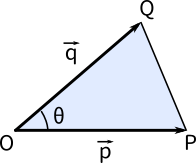面積素とパラメータ ベクトル解析 基礎からの数学入門	面積素とパラメータ ベクトル解析 基礎からの数学入門	面積素とパラメータ ベクトル解析 基礎からの数学入門
面積素とパラメータ ベクトル解析 基礎からの数学入門	面積素とパラメータ ベクトル解析 基礎からの数学入門	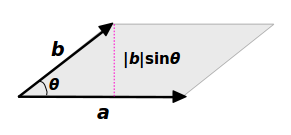面積素とパラメータ ベクトル解析 基礎からの数学入門
面積素とパラメータ ベクトル解析 基礎からの数学入門	面積素とパラメータ ベクトル解析 基礎からの数学入門	面積素とパラメータ ベクトル解析 基礎からの数学入門
面積素とパラメータ ベクトル解析 基礎からの数学入門	面積素とパラメータ ベクトル解析 基礎からの数学入門	面積素とパラメータ ベクトル解析 基礎からの数学入門
面積素とパラメータ ベクトル解析 基礎からの数学入門	面積素とパラメータ ベクトル解析 基礎からの数学入門	面積素とパラメータ ベクトル解析 基礎からの数学入門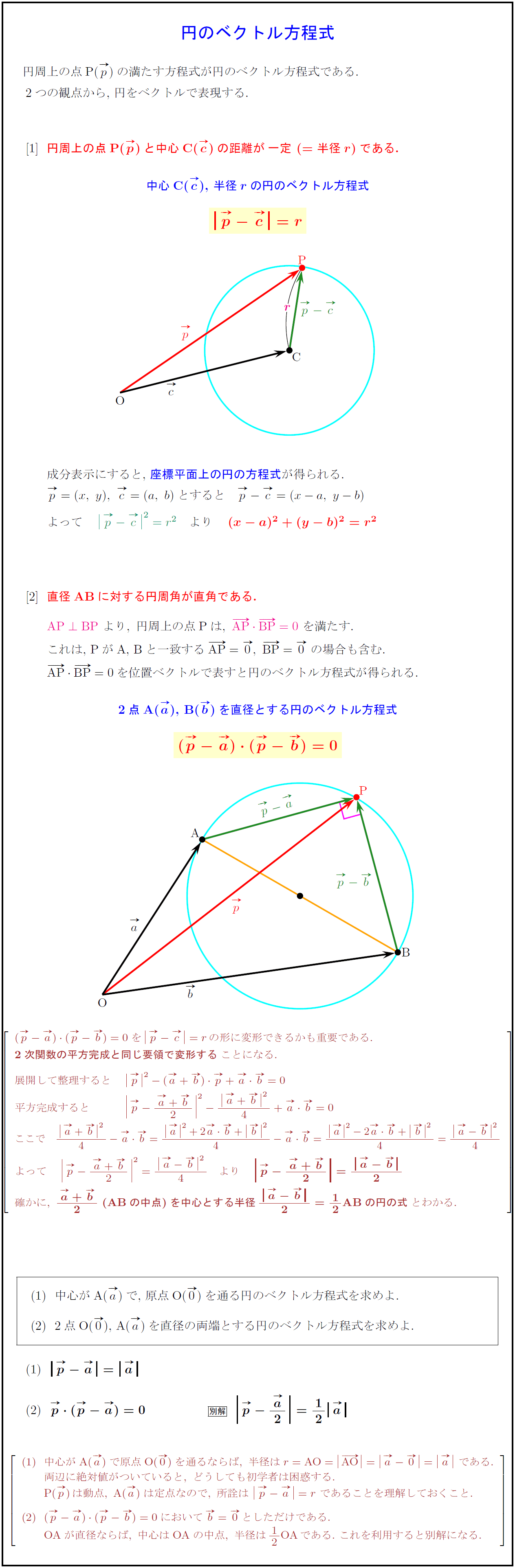
面積素とパラメータ ベクトル解析 基礎からの数学入門	面積素とパラメータ ベクトル解析 基礎からの数学入門	面積素とパラメータ ベクトル解析 基礎からの数学入門
面積素とパラメータ ベクトル解析 基礎からの数学入門	面積素とパラメータ ベクトル解析 基礎からの数学入門	面積素とパラメータ ベクトル解析 基礎からの数学入門
面積素とパラメータ ベクトル解析 基礎からの数学入門	面積素とパラメータ ベクトル解析 基礎からの数学入門	面積素とパラメータ ベクトル解析 基礎からの数学入門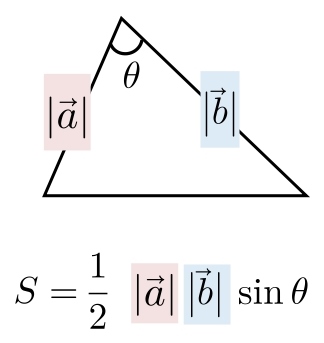
面積素とパラメータ ベクトル解析 基礎からの数学入門	面積素とパラメータ ベクトル解析 基礎からの数学入門	面積素とパラメータ ベクトル解析 基礎からの数学入門
面積素とパラメータ ベクトル解析 基礎からの数学入門	面積素とパラメータ ベクトル解析 基礎からの数学入門	面積素とパラメータ ベクトル解析 基礎からの数学入門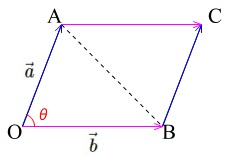
面積素とパラメータ ベクトル解析 基礎からの数学入門	面積素とパラメータ ベクトル解析 基礎からの数学入門	面積素とパラメータ ベクトル解析 基礎からの数学入門
面積素とパラメータ ベクトル解析 基礎からの数学入門	面積素とパラメータ ベクトル解析 基礎からの数学入門	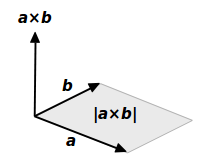面積素とパラメータ ベクトル解析 基礎からの数学入門
面積素とパラメータ ベクトル解析 基礎からの数学入門	面積素とパラメータ ベクトル解析 基礎からの数学入門	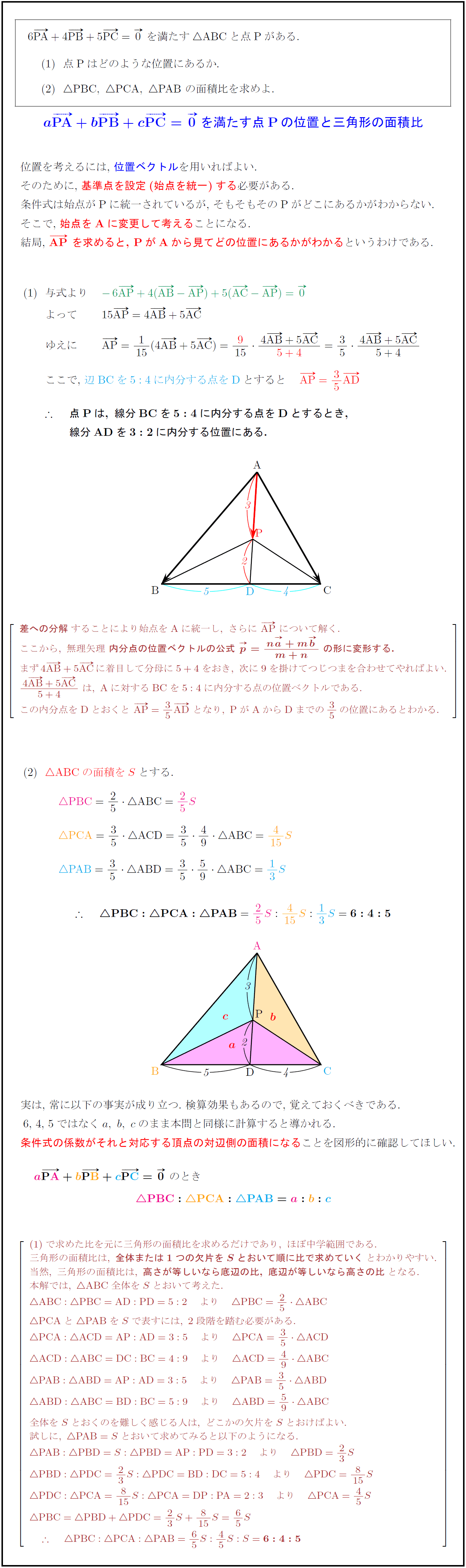面積素とパラメータ ベクトル解析 基礎からの数学入門
面積素とパラメータ ベクトル解析 基礎からの数学入門	面積素とパラメータ ベクトル解析 基礎からの数学入門	面積素とパラメータ ベクトル解析 基礎からの数学入門
面積素とパラメータ ベクトル解析 基礎からの数学入門	面積素とパラメータ ベクトル解析 基礎からの数学入門	面積素とパラメータ ベクトル解析 基礎からの数学入門
面積素とパラメータ ベクトル解析 基礎からの数学入門	面積素とパラメータ ベクトル解析 基礎からの数学入門	面積素とパラメータ ベクトル解析 基礎からの数学入門
面積素とパラメータ ベクトル解析 基礎からの数学入門	面積素とパラメータ ベクトル解析 基礎からの数学入門	面積素とパラメータ ベクトル解析 基礎からの数学入門
面積素とパラメータ ベクトル解析 基礎からの数学入門	面積素とパラメータ ベクトル解析 基礎からの数学入門	面積素とパラメータ ベクトル解析 基礎からの数学入門
面積素とパラメータ ベクトル解析 基礎からの数学入門	面積素とパラメータ ベクトル解析 基礎からの数学入門	面積素とパラメータ ベクトル解析 基礎からの数学入門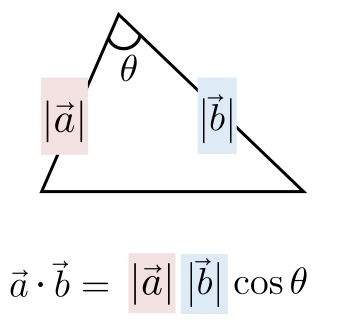
面積素とパラメータ ベクトル解析 基礎からの数学入門	面積素とパラメータ ベクトル解析 基礎からの数学入門	面積素とパラメータ ベクトル解析 基礎からの数学入門
面積素とパラメータ ベクトル解析 基礎からの数学入門	面積素とパラメータ ベクトル解析 基礎からの数学入門	面積素とパラメータ ベクトル解析 基礎からの数学入門
面積素とパラメータ ベクトル解析 基礎からの数学入門	面積素とパラメータ ベクトル解析 基礎からの数学入門	面積素とパラメータ ベクトル解析 基礎からの数学入門
面積素とパラメータ ベクトル解析 基礎からの数学入門	面積素とパラメータ ベクトル解析 基礎からの数学入門	面積素とパラメータ ベクトル解析 基礎からの数学入門
面積素とパラメータ ベクトル解析 基礎からの数学入門	面積素とパラメータ ベクトル解析 基礎からの数学入門	面積素とパラメータ ベクトル解析 基礎からの数学入門
面積素とパラメータ ベクトル解析 基礎からの数学入門	面積素とパラメータ ベクトル解析 基礎からの数学入門	面積素とパラメータ ベクトル解析 基礎からの数学入門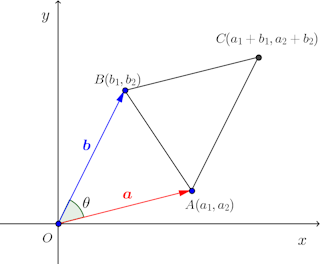
面積素とパラメータ ベクトル解析 基礎からの数学入門	面積素とパラメータ ベクトル解析 基礎からの数学入門	面積素とパラメータ ベクトル解析 基礎からの数学入門
面積素とパラメータ ベクトル解析 基礎からの数学入門	面積素とパラメータ ベクトル解析 基礎からの数学入門

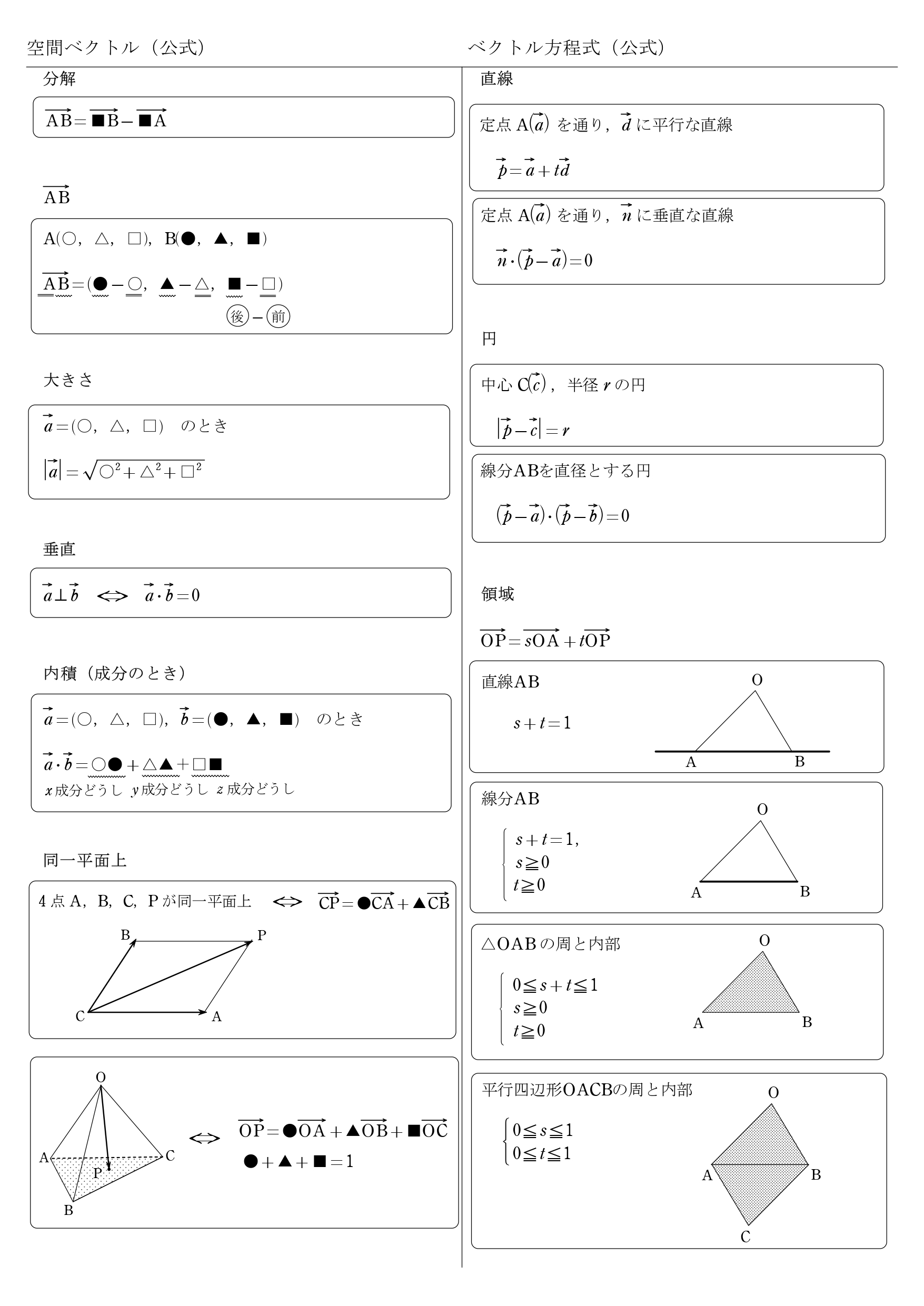
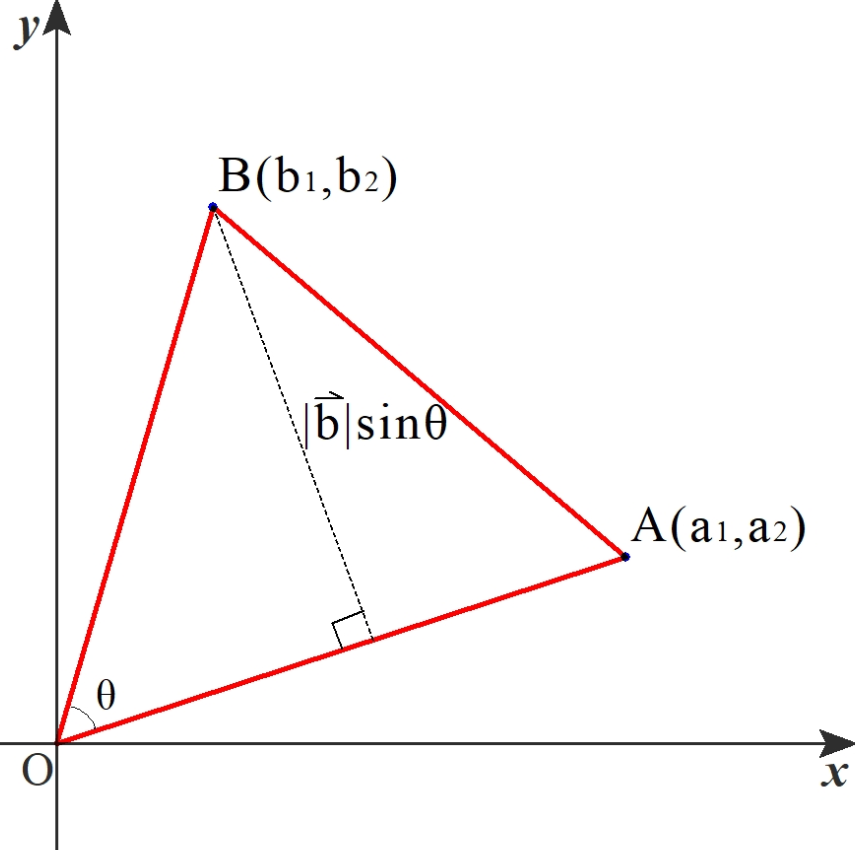
ベクトルの成分と三角形の面積 先ほどの式を、成分で考えてみましょう。 すると、これもきれいな式が得られます。 b = (b1,b2) b → = ( b 1, b 2) として、ルートの中を計算していきましょう。 基本ベクトルの内積と成分 で見た内容などを使って b)2 = (a2前回にて線積分の概要と例題を取り扱った。 今回はその続きで、面積分の概要を眺め、問題の解き方を解説していく。概要 面積分も線積分と同様にベクトル場に対して実行する積分である。 線積分との違いは「面」と書かれている通り、ある座標系に存在する

Incoming Term: 面積 公式 ベクトル, 平行四辺形 面積 公式 ベクトル, ベクトル 面積 公式 覚え方, ベクトル 面積 公式 空間, ベクトル 内積 面積 公式, ベクトル 面積 公式 サイン,